Axon: The STICK Software Development Kit
The brain encodes information using precise spike timing, not just rates or continuous activations. Inspired by this, Axon is a software framework for building, simulating, and compiling symbolic spiking neural networks (SNNs) using the STICK (Spike Time Interval Computational Kernel) model.
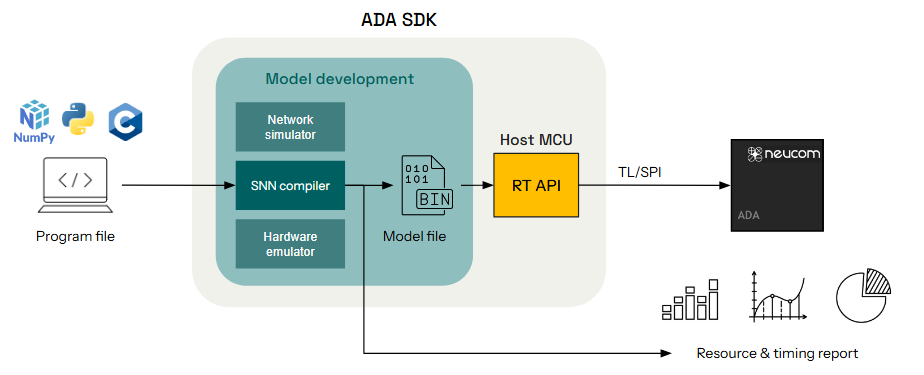
Axon provides an end-to-end pipeline for deploying interval-coded SNNs to ultra-low-power neuromorphic hardware, such as the ADA chip. It is built for embedded deployment, yet flexible enough for rapid prototyping and evaluation on general-purpose CPUs.
Axon includes:
- A Python-based simulator for cycle-accurate emulation of interval-coded symbolic computation.
- A hardware-aware compiler that translates modular spiking circuits into a compact binary model format.
- A runtime API (RT API) to interface with the ADA coprocessor over TL-UL or SPI.
- Tools for resource reporting, cycle estimation, and model profiling.
If you’re building symbolic SNNs for embedded inference, control, or cryptographic tasks, Axon bridges software models with neuromorphic execution.
Axon Structure
| Component | Description |
|---|---|
axon.simulator | Spiking network simulator with support for STICK primitives and gating logic |
axon.compiler | Converts network graphs into optimized model binaries for ADA execution |
axon.utils | Data loading, waveform generation, testbench scripting |
Requirements
Axon is built in Python and depends on:
- Python ≥ 3.8
- NumPy
- NetworkX
- TQDM
- Matplotlib (for visual debugging)
- PyVCD (optional, for waveform output)
To simulate hardware behavior with Verilator (optional for advanced use):
- Verilator ≥ 5.034
- C++17 toolchain
Installation
Install the SDK from source:
git clone https://github.com/neucom/axon.git
cd axon
pip install -e .
Example: Multiplication Network
from axon.simulator import Simulator
from axon.networks import MultiplierNetwork
from axon.utils import encode_interval
# Encode input spikes
x1_spikes = encode_interval(0.4)
x2_spikes = encode_interval(0.25)
# Build network
net = MultiplierNetwork()
sim = Simulator(net)
# Inject spikes and simulate
sim.inject(x1=x1_spikes, x2=x2_spikes)
sim.run()
# View results
sim.plot_chronogram()
Citation
If you use Axon or ADA in your research, please cite:
@misc{axon2025,
title = {Axon: A Software Development Kit for Symbolic Spiking Networks},
author = {Neucom},
howpublished = {\url{https://github.com/neucom/axon}},
year = {2025}
}
Contact
If you’re working with Axon or STICK-based hardware and want to share your application, request features, or report issues, reach out via GitHub Issues or contact the Neucom team at contact@neucom.ai.

Axon SDK – Getting Started
A streamlined guide to get you up and running quickly with the Python-based STICK (Spike Time Interval Computational Kernel) simulator and toolkit.
Requirements
- Python 3.11+
- pip
- Recommended packages (auto-installed):
- numpy
- networkx
- tqdm
- matplotlib
Installation
Using pip
To install the Axon SDK, simply run:
pip install axon-sdk
Alternatively, install axon-sdk in editable mode (ideal for development):
git clone https://github.com/neucom/axon-sdk.git
cd axon-sdk
pip install -e .
Interval Coding in Axon
This document explains how Axon implements the interval-based encoding and computation as defined by the STICK (Spike Time Interval Computational Kernel) model.
1. Neuron & Synapse Model
Axon uses a simplified Integrate-and-Fire neuron model, supporting three synapse types:
- V-synapses: instantaneously modify membrane potential (excitatory
w_e = V_tor inhibitoryw_i = -V_t) - gₑ-synapses: conductance-based, model temporal integration
- g_f-synapses: fast-gated conductance-based
Each synapse includes a configurable delay (≥ T_syn, the minimal delay) :contentReference[oaicite:1]{index=1}.
2. Interval-Based Value Encoding
Values x ∈ [0,1] are encoded in the time difference Δt between two spikes:
Δt = T_min + x · T_cod
x = (Δt − T_min) / T_cod
where:
- T_min: minimum time difference (e.g., 1 ms)
- T_cod: coding interval (e.g., 10 ms)
- Δt: time difference between two spikes
3. Interval-Based Computation
Spiking networks can be build to process these interval-encoded values. The network dynamics are governed by the synaptic weights and delays, allowing for complex computations based on the timing of spikes.
- Value
xis represented by timing between spikes Δt. - Spiking networks manipulate these intervals via synaptic delays, integration, and gating, executing operations like addition, multiplication, and memory.
4. Memory & Control Flow Patterns
Axon includes reusable network patterns for symbolic SNN algorithms, such as:
4.1 Volatile Memory
-
Uses an accumulator neuron (acc) to store value in membrane potential.
-
Spike-to-store encodes interval into potential; recall emits output with the same interval once.
Neuron Model in Axon
This document details the spiking neuron model used in Axon, which implements the STICK (Spike Time Interval Computational Kernel) computational paradigm. It emphasizes temporal coding, precise spike timing, and synaptic diversity for symbolic computation.
1. Overview
Axon simulates event-driven, integrate-and-fire neurons with:
- Millisecond-precision spike timing
- Multiple synapse types with distinct temporal effects
- Explicit gating to modulate temporal dynamics
The base classes are:
AbstractNeuron: defines core membrane equationsExplicitNeuron: tracks spike times and enables connectivitySynapse: defines delayed, typed connections between neurons
2. Neuron Dynamics
Each neuron maintains four internal state variables:
| Variable | Description |
|---|---|
V | Membrane potential (mV) |
ge | Persistent excitatory input (constant) |
gf | Fast exponential input (gated) |
gate | Binary gate controlling gf integration |
The membrane potential evolves according to:
\tau_m \frac{dV}{dt} = g_e + \text{gate} \cdot g_f
where:
τmis the membrane time constantg_eis the persistent excitatory inputg_fis the fast decaying input, gated bygateThe neuron spikes whenVexceeds a thresholdVt, at which point it emits a spike and resets its state. After a spike, the neuron resets:
V → Vreset ge → 0 gf → 0 gate → 0
This reset guarantees clean integration for subsequent intervals.
4. Synapse Types
Axon supports four biologically inspired synapse types:
| Type | Effect |
|---|---|
V | Immediate change in membrane: V += w |
ge | Adds persistent drive: ge += w |
gf | Adds fast decaying drive: gf += w |
gate | Toggles gate flag (w = ±1) to activate gf |
Each synapse also includes a configurable delay, enabling precise temporal computation.
5. Implementation Summary
Class: AbstractNeuron
- Implements update logic for
ge,gf, andgate - Defines
update_and_spike(dt)for simulation cycles - Supports
receive_synaptic_event(type, weight)
Class: ExplicitNeuron
- Inherits from
AbstractNeuron - Tracks:
spike_times[]out_synapses[]
- Implements
reset()after spike emission
Class: Synapse
- Defines:
pre_neuron,post_neuronweight,delay,type
- Used to construct event-driven spike queues with delay accuracy
6. Temporal Coding & Integration
This neuron model is designed for interval-coded values. Time intervals between spikes directly encode numeric values.
Integration periods in neurons align with computation windows:
ge: accumulates static value during inter-spike intervalgf+gate: used for exponential/logarithmic timingV: compares integrated potential to threshold for spike emission
These dynamics enable symbolic operations such as memory, arithmetic, and differential equation solving.
7. Numerical Parameters
Typical parameter values used in Axon:
| Parameter | Value | Meaning |
|---|---|---|
Vt | 10.0 mV | Spiking threshold |
Vreset | 0.0 mV | Voltage after reset |
τm | 100.0 ms | Membrane integration constant |
τf | 20.0 ms | Fast synaptic decay constant |
Units are in milliseconds or millivolts, matching real-time symbolic processing and neuromorphic feasibility.
8. Benefits of This Model
- Compact: Minimal neurons required for functional blocks
- Precise: Accurate sub-millisecond spike-based encoding
- Composable: Modular design supports hierarchical circuits
- Hardware-Compatible: Ported to digital integrate-and-fire cores like ADA
Neuron Model Animation
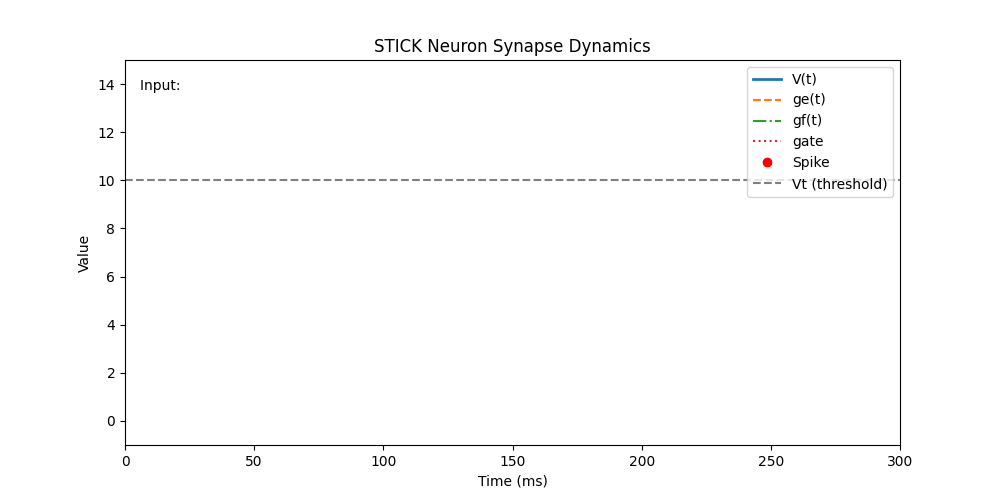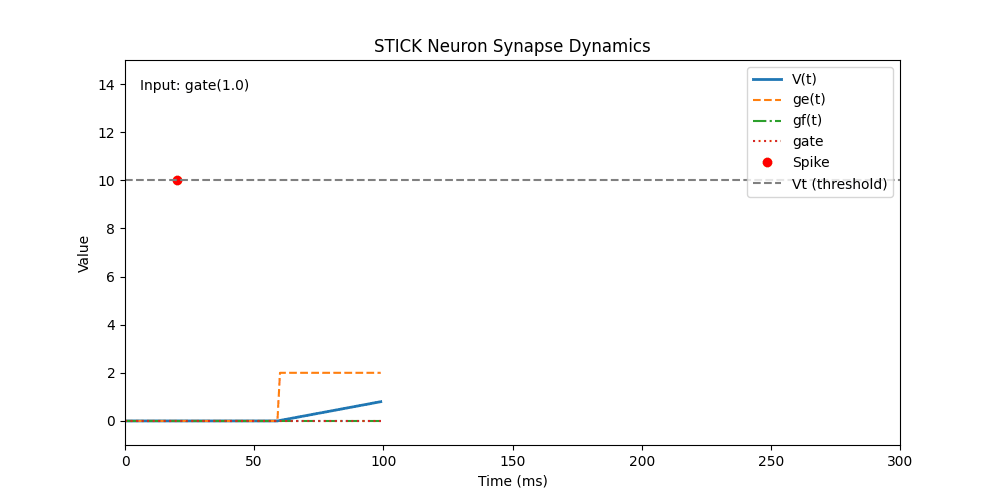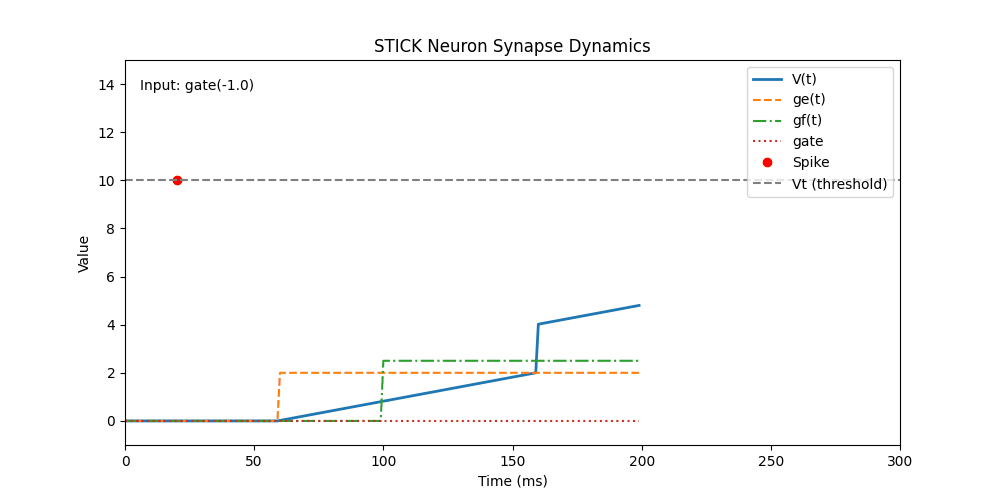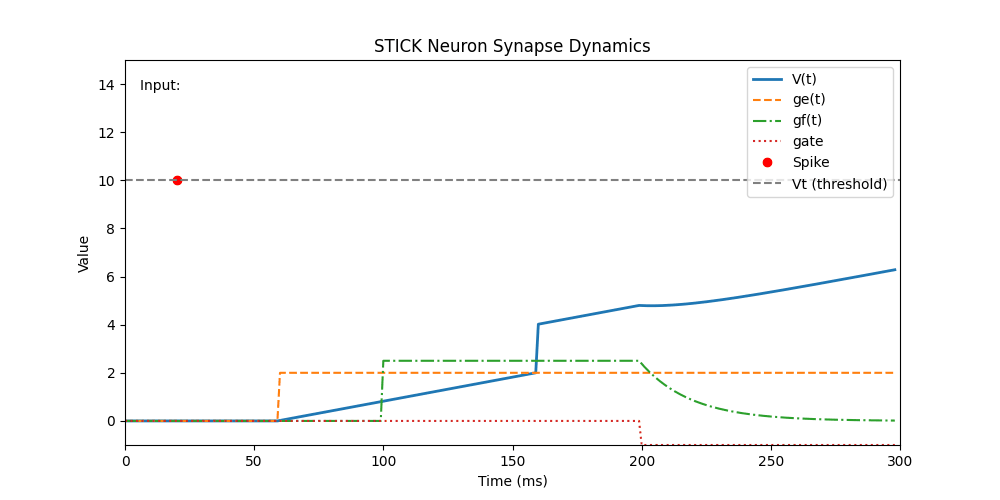 This animation demonstrates how a single STICK neuron responds over time to different synaptic inputs. Each input type (
This animation demonstrates how a single STICK neuron responds over time to different synaptic inputs. Each input type (V, ge, gf, gate) produces distinct changes in membrane dynamics. The neuron emits a spike when its membrane potential V(t) reaches the threshold Vt = 10.0 mV, after which it resets.
Synapse Events Timeline
| Time (ms) | Type | Value | Description |
|---|---|---|---|
t = 20 | V | 10.0 | Instantaneously pushes V to threshold: triggers immediate spike |
t = 60 | ge | 2.0 | Applies constant integration current: slow, linear voltage increase |
t = 100 | gf | 2.5 | Adds fast-decaying input, gated via gate = 1 at same time |
t = 160 | V | 2.0 | Small, instant boost to V |
t = 200 | gate | -1.0 | Disables exponential decay pathway by zeroing the gate signal |
Event-by-Event Explanation
t = 20 ms — V(10.0)
- A V-synapse adds +10.0 mV to
Vinstantly. - Since
Vt = 10.0, this causes immediate spike. - The neuron resets:
V → 0,ge, gf, gate → 0.
Effect: Demonstrates a direct spike trigger via instantaneous voltage jump.
t = 60 ms — ge(2.0)
- A ge-synapse applies constant input current.
- Voltage rises linearly over time.
- Alone, this isn’t sufficient to reach
Vt, so no spike occurs yet.
Effect: Shows the smooth effect of continuous integration from ge-type input.
t = 100 ms — gf(2.5) and gate(1.0)
- A gf-synapse delivers fast-decaying input current.
- A gate-synapse opens the gate (
gate = 1), activatinggfdynamics. - Voltage rises nonlinearly as
gfinitially dominates, then decays. - Combined effect from earlier
geandgfcauses a spike shortly after.
Effect: Demonstrates exponential integration (gf) gated for a temporary burst.
t = 160 ms — V(2.0)
- A small V-synapse bump of +2.0 mV occurs.
- This is not enough to cause a spike, but it shifts
Vupward instantly.
Effect: Shows subthreshold perturbation from a V-type synapse.
t = 200 ms — gate(-1.0)
- The gate is closed (
gate = 0), disablinggfdecay term. - Any remaining
gfis no longer integrated intoV.
Effect: Demonstrates control logic: gf is disabled, computation halts.
Summary of Synapse Effects
| Synapse Type | Behavior |
|---|---|
V | Instantaneous jump in membrane potential V |
ge | Slow, steady increase in V over time |
gf + gate | Fast, nonlinear voltage rise due to exponential dynamics |
gate | Controls whether gf affects the neuron at all |
Spike Dynamics
When V ≥ Vt, the neuron:
- Spikes
- Logs spike time
- Resets all internal state to baseline
You can see these spikes as red dots at the threshold line in the animation.
References
- Lagorce & Benosman (2015): Spike Time Interval Computational Kernel
- Axon SDK Source:
- Neuron model:
axon/elements.py - Event logic:
axon/events.py - Simulator integration:
axon/simulator.py
- Neuron model:
Synapse Types in Axon
This document outlines the synapse model implemented in Axon, inspired by the STICK (Spike Time Interval Computational Kernel) framework. Synapses in Axon are the primary mechanism for transmitting and transforming spike-encoded values in time.
1. Overview
Each synapse in Axon connects a presynaptic neuron to a postsynaptic neuron, applying a time-delayed effect based on its type, weight, and delay.
All synaptic interactions are event-driven and time-resolved, respecting the temporal precision of interval coding.
2. Supported Synapse Types
Axon supports four distinct types of synaptic interactions:
| Type | Symbol | Action on Postsynaptic Neuron |
|---|---|---|
V | – | Adds directly to membrane potential: V ← V + w |
ge | – | Adds constant input current: ge ← ge + w |
gf | – | Adds to exponentially decaying input current: gf ← gf + w |
gate | ±1 | Activates or deactivates gf dynamics: gate ← gate + w |
Each synapse includes a delay value d (in ms), which specifies when the effect reaches the target neuron after a spike.
3. Synapse Type Descriptions
V-Synapse
- Function: Direct voltage jump
- Use Cases:
- Trigger immediate spiking
- Apply inhibition (if
w < 0) - Detect coincidences
- Equation:
V ← V + w
### ge-Synapse
- **Function**: Adds persistent excitatory current
- **Use Cases**:
- Provide sustained excitatory drive
- Enable long-term potentiation (LTP)
- **Equation**:
```python
ge ← ge + w
```
### gf-Synapse
- **Function**: Adds fast decaying excitatory current
- **Use Cases**:
- Provide rapid excitatory input
- Enable short-term plasticity (STP)
- **Equation**:
```python
gf ← gf + w
```
### gate-Synapse
- **Function**: Toggles gating for `gf` dynamics
- **Use Cases**:
- Activate or deactivate `gf` input
- Control temporal dynamics of the neuron
- **Equation**:
```python
gate ← gate + w
```
## 4. Synapse Delay
Each synapse has a **delay** parameter `d` (in milliseconds) that specifies how long after the presynaptic spike the effect will be applied to the postsynaptic neuron. This delay allows for precise temporal computation and modeling of biological synaptic transmission.
Every synapse includes a delay d (in milliseconds):
Represents transmission latency
Defines when the effect arrives at the postsynaptic neuron
Supports precise spike scheduling and coordination
## 5. Use In Computation
Synapse types form the basis of STICK-based operations in Axon:
| Operation | Synapse Type(s) Used |
| --------------- | -------------------- |
| Memory Storage | `ge` |
| Memory Recall | `V` |
| Log/Exp | `gf` + `gate` |
| Control Flow | `gate`, `V` |
| Spike Synchrony | `V` + delay routing |
They are composable and programmable, enabling symbolic logic, arithmetic, and learning mechanisms entirely through spike timing.
## 5. Implementation Summary
```python
Synapse(
pre_neuron: ExplicitNeuron,
post_neuron: ExplicitNeuron,
weight: float,
delay: float,
synapse_type: str # 'V', 'ge', 'gf', or 'gate'
)
Events are scheduled based on the synapse type and delay, allowing for precise control over the timing of postsynaptic effects.
Synaptic effects are handled in:
elements.py->AbstractNeuron.receive_synaptic_event(...)events.py->SpikeEventQueue.add_event()
Network Composition & Orchestration in Axon
This guide describes how to compose, connect, and orchestrate symbolic SNN structures in Axon using the STICK model—enabling modular designs, reusable components, and seamless simulation-to-hardware workflows.
1. Modular Network Architecture
Axon encourages defining networks as combinations of modules:
- Atomic modules: basic units (e.g.,
Adder,Multiplier,MemoryUnit) - Composite modules: built by connecting atomic or other composite units
Each module exposes:
- Input ports (spike sources)
- Output ports (spike sinks)
- Internal logic (neurons, synapses, gating)
Example
from axon.networks import Adder, Multiplier
from axon.composition import compose
add = Adder(name='add1')
mul = Multiplier(name='mul1')
net = compose([add, mul],
connections=[('add1.out', 'mul1.in1'),
('external.x', 'add1.in1'),
('external.y', 'add1.in2'),
('external.z', 'mul1.in2')])
2. Connection Patterns
Axon supports flexible connection patterns between modules:
- Direct connections: link output of one module to input of another
- Broadcasting: send output to multiple inputs
Functional Networks in Axon SDK
The axon_sdk.networks.functional module implements symbolic arithmetic and nonlinear operations using biologically inspired spiking neuron circuits. These circuits follow the STICK (Spike Time Interval Computational Kernel) framework, encoding and transforming values as spike intervals.
Included Functional Modules
| File | Operation |
|---|---|
adder.py | Signed 2-input addition |
subtractor.py | Signed subtraction via negate + add |
multiplier.py | Multiplication using log and exp |
signed_multiplier.py | Signed version of multiplier.py |
scalar_multiplier.py | Multiply by fixed constant |
linear_combination.py | Weighted linear sum |
natural_log.py | Natural logarithm computation |
exponential.py | Exponential function |
divider.py | Approximate division using exp/log |
integrator.py | Continuous summation over time |
signflip.py | Sign inversion (negation) |
Each of these networks is implemented as a subclass of SpikingNetworkModule.
Case Study: Exponential Function (exponential.py)
Purpose
implements the exponential function ( e^x ) using a spiking network.
Where x ∈[0,1] is encoded as a spike interval, and the network emits an output spike interval corresponding to e^x also encoded as an interspike time.
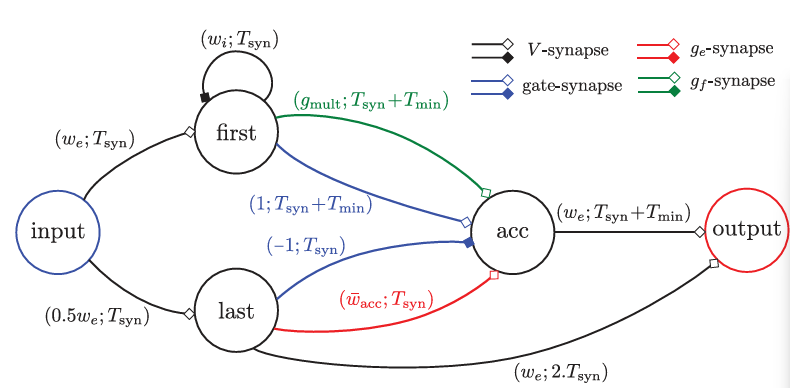
Construction
| Neuron | Role |
|---|---|
input | Receives spike pair (encodes x) |
first | Fires on first spike |
last | Fires on second spike |
acc | Performs gated exponential integration |
output | Emits interval representing result |
Principle
As described in the STICK paper (Lagorce et al. 2015) exponential encoding uses gated exponential decay to map input to output time:
tf * d/dt(gf) = -gf
The accumulated voltage V(t) rises under:
tm * dV/dt = gate * gf
firstactivatesgfonaccwith delayTmin, setting exponential decay in motion.gate=1is enabled at the same time to allowgfto contribute toV(t).lastdisables gate (gate=-1) and adds a fixedgeto pushacctowards the threshold and spiking.acc->output: OnceV(t)exceeds threshold,outputemits a spike with interval equal to the accumulated voltage.
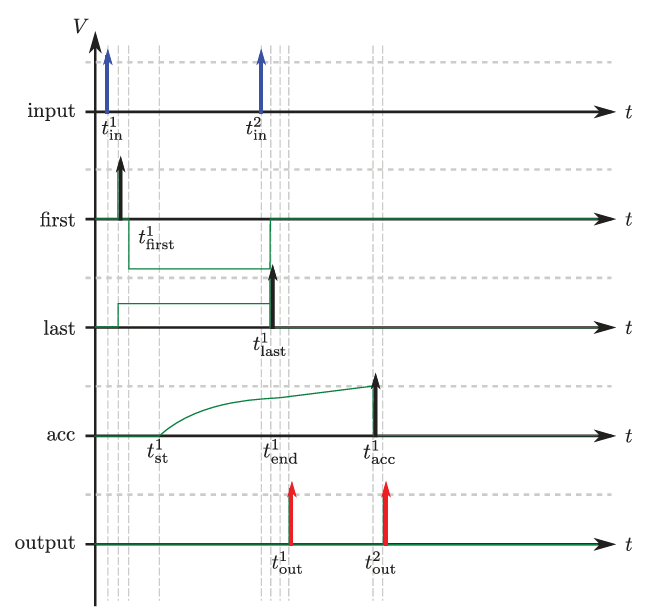
self.connect_neurons(self.first, self.acc, "gf", gmult, Tsyn + Tmin)
self.connect_neurons(self.first, self.acc, "gate", 1, Tsyn + Tmin)
self.connect_neurons(self.last, self.acc, "gate", -1.0, Tsyn)
self.connect_neurons(self.last, self.acc, "ge", wacc_bar, Tsyn)
The delay of the output spike is computed as:
$$ T_{\text{out}} = T_{\text{min}} + T_{\text{cod}} \cdot e^{-x \cdot T_{\text{cod}} / \tau_f} $$
This ensures that the spike interval output represents:
$$ y = e^x $$
encoded again via interspike time.
Simulation Result Example
Input value: 0.5
Expected exp value: 1.6487
Decoded exp value: 1.6332
Expected exp delay: 49.3 ms
Measured exp delay: 49.7 ms
Flow for Implementing New Stick Networks
- Subclass
SpikingNetworkModule
class MyNetwork(SpikingNetworkModule):
def __init__(self, encoder, module_name=None):
super().__init__(module_name)
...
- Define neurons:
self.inp = self.add_neuron(Vt, tm, tf, neuron_name="inp")
- Connect neurons with appropriate synapses:
V: Jump voltagege: Constant integrationgf: Exponentialgate: control input
self.connect_neurons(src, tgt, "ge", weight, delay)
Full Exponential Network Example
from axon_sdk.primitives import (
SpikingNetworkModule,
DataEncoder,
)
import math
from typing import Optional
class ExponentialNetwork(SpikingNetworkModule):
def __init__(self, encoder: DataEncoder, module_name: Optional[str] = None) -> None:
super().__init__(module_name)
self.encoder = encoder
# Parameters
Vt = 10.0
tm = 100.0
self.tf = 20.0
Tsyn = 1.0
Tmin = encoder.Tmin
we = Vt
wi = -Vt
gmult = (Vt * tm) / self.tf
wacc_bar = Vt * tm / encoder.Tcod # To ensure V = Vt at Tcod
# Neurons
self.input = self.add_neuron(Vt, tm, self.tf, neuron_name="input")
self.first = self.add_neuron(Vt, tm, self.tf, neuron_name="first")
self.last = self.add_neuron(Vt, tm, self.tf, neuron_name="last")
self.acc = self.add_neuron(Vt, tm, self.tf, neuron_name="acc")
self.output = self.add_neuron(Vt, tm, self.tf, neuron_name="output")
# Connections from input neuron
self.connect_neurons(self.input, self.first, "V", we, Tsyn)
self.connect_neurons(self.input, self.last, "V", 0.5 * we, Tsyn)
# Inhibit first after spike
self.connect_neurons(self.first, self.first, "V", wi, Tsyn)
# Exponential computation:
# 1. First spike → apply gf with delay = Tsyn + Tmin
self.connect_neurons(self.first, self.acc, "gf", gmult, Tsyn + Tmin)
self.connect_neurons(self.first, self.acc, "gate", 1, Tsyn + Tmin)
# 2. Last spike → open gate
self.connect_neurons(self.last, self.acc, "gate", -1.0, Tsyn)
# 3. Last spike → add ge to trigger spike after ts
self.connect_neurons(self.last, self.acc, "ge", wacc_bar, Tsyn)
# Readout to output
self.connect_neurons(self.acc, self.output, "V", we, Tsyn + Tmin)
self.connect_neurons(self.last, self.output, "V", we, 2 * Tsyn)
def expected_exp_output_delay(x, encoder: DataEncoder, tf):
try:
delay = encoder.Tcod * math.exp(-x * encoder.Tcod / tf)
Tout = encoder.Tmin + delay
return Tout
except:
return float("nan")
def decode_exponential(output_interval, encoder: DataEncoder, tf):
return ((output_interval - encoder.Tmin) / encoder.Tcod) ** (-tf / encoder.Tcod)
if __name__ == "__main__":
from axon_sdk import Simulator
encoder = DataEncoder(Tmin=10.0, Tcod=100.0)
net = ExponentialNetwork(encoder)
sim = Simulator(net, encoder, dt=0.01)
value = 0.5
sim.apply_input_value(value, neuron=net.input, t0=10)
sim.simulate(150)
output_spikes = sim.spike_log.get(net.output.uid, [])
if len(output_spikes) == 2:
out_interval = output_spikes[1] - output_spikes[0]
print(f"Input value: {value}")
print(
f"Expected exp value: {math.exp(value)}, decoded exp value {decode_exponential(out_interval, encoder, net.tf)}, "
)
print(
f"Expected exp delay: {expected_exp_output_delay(value, encoder, net.tf):.3f} ms"
)
print(f"Measured exp delay: {out_interval:.3f} ms")
else:
print(f"Expected 2 output spikes, got {len(output_spikes)}")
Axon Simulator Engine
The Axon simulator executes symbolic spiking neural networks (SNNs) built with the STICK (Spike Time Interval Computational Kernel) model. This document describes the simulation engine’s architecture, parameters, workflow, and features.
1. Purpose
The Simulator class provides a discrete-time, event-driven environment to simulate:
- Spiking neuron dynamics
- Synaptic event propagation
- Interval-based input encoding and output decoding
- Internal logging of voltages and spikes
It is optimized for symbolic, low-rate temporal computation rather than high-frequency biological modeling.
2. Core Components
| Component | Description |
|---|---|
net | The user-defined spiking network (a SpikingNetworkModule) |
dt | Simulation timestep in seconds (default: 0.001) |
event_queue | Priority queue managing scheduled synaptic events |
encoder | Object for encoding/decoding interval-coded values |
spike_log | Maps neuron UIDs to their spike timestamps |
voltage_log | Records membrane voltage per neuron per timestep |
3. Simulation Loop
The simulator proceeds in dt-sized increments for a specified duration:
-
Event Queue Check
All scheduled events due at timetare popped. -
Synaptic Updates
Each event updates the target neuron’s state (V,ge,gf, orgate). -
Neuron Updates
Each affected neuron is numerically integrated using:
V += (ge + gate * gf) * dt / tau_m
where tau_m is the membrane time constant.
- Spike Detection & Reset
IfV ≥ Vt, the neuron spikes:
V ← Vreset,ge ← 0,gf ← 0,gate ← 0- All outgoing synapses generate future spike events
- Activity Tracking
Neurons with non-zeroge,gf, orgateare marked active for the next step.
4. Configuration Knobs
| Parameter | Description | Default |
|---|---|---|
dt | Time resolution per step (in seconds) | 0.001 (1 ms) |
Tmin | Minimum interspike delay in encoding | 10.0 ms |
Tcod | Encoding range above Tmin | 100.0 ms |
simulation_time | Total simulation duration (in seconds) | user-defined |
These settings are defined at the simulator or encoder level depending on purpose.
5. Inputs & Injection
apply_input_value(value, neuron, t0=0)
Injects a scalar value ∈ [0, 1] into a neuron via interval-coded spike pair.
apply_input_spike(neuron, t)
Injects a single spike into a neuron at exact time t.
6. Output Decoding
To read results from signed STICK outputs:
from axon.simulator import decode_output
value = decode_output(simulator, reader)
Decodes interval between two spikes on either the + or − output neuron
Returns a signed scalar in [−1, 1] (scaled by reader.normalization)
7. Logging and Visualization
The simulator maintains:
spike_log: Maps neuron UIDs to spike timestamps with: {neuron_uid: [t0, t1, …]}voltage_log: Maps neuron UIDs to their membrane voltages at each timestep with: {neuron_uid: [V0, V1, …]}
Optional visualization can be enabled by setting VIS=1 in your environment.
sim.launch_visualization()
plot_chronogram(): Spike raster and voltage tracesvis_topology(): Interactive network topology visualization
8. Design Flow
- Define Network: Create a
SpikingNetworkModulewith neurons and synapses.
from axon_sdk.network import SpikingNetworkModule
net = SpikingNetworkModule()
- Instantiate Encoder: Create an encoder for interval coding.
from axon_sdk.encoder import DataEncoder
encoder = DataEncoder(Tmin=10.0, Tcod=100.0)
- Instantiate Simulator: Create a
Simulatorinstance with the network and parameters.
sim = Simulator(net, encoder dt=0.001)
- Apply Inputs: Use
apply_input_value()orapply_input_spike()to inject data.
sim.apply_input_value(0.5, neuron_uid, t0=0)
- Run Simulation: Execute the simulation for a specified duration of timesteps.
sim.run(simulation_time=100)
- Analyze Outputs: Use
decode_output()to read results from the simulation.
value = sim.decode_output(reader)
Example Usage
from axon_sdk.simulator import Simulator
from axon_sdk.networks import MultiplierNetwork
from axon_sdk.utils import encode_interval
net = MultiplierNetwork()
encoder = DataEncoder()
sim = Simulator(net, encoder, dt=0.001)
a, b = 0.4, 0.25
sim.apply_input_value(a, net.input1)
sim.apply_input_value(b, net.input2)
sim.simulate(simulation_time=0.5)
sim.plot_chronogram()
11. Summary
-
Event-driven, millisecond-resolution simulator
-
Supports interval-coded STICK networks
-
Accurate logging of all internal neuron dynamics
-
Integrates seamlessly with compiler/runtime interfaces
Data Encoding in Axon
The DataEncoder class is responsible for converting scalar values into inter-spike intervals (ISIs) and decoding them back. This functionality is central to how Axon implements symbolic computation using the STICK (Spike Time Interval Computational Kernel) framework.
1. Concept
In STICK-based networks, numerical values are encoded not in voltage amplitude or spike rate, but in the time difference between two spikes. This allows for:
- High temporal resolution
- Symbolic logic without rate coding
- Hardware-friendly encoding (e.g., for ADA)
2. Encoding Equation
A normalized value ( x \n [0, 1] ) is encoded as a spike interval:
Δt = Tmin + x * Tcod
where:
- ( Tmin ) is the minimum interval (e.g., 1 ms
- ( Tcod ) is the coding range (e.g., 100 ms)
- ( dt ) is the resulting inter-spike interval (ISI)
Example:
Δt = 10 + 0.4 * 100 = 50 ms
Decoding Equation
To decode a spike interval back into a value:
x = (interval - Tmin) / Tcod
where:
intervalis the time difference between two spikes. This is the inverse of the encoder.
3. DataEncoder Class
The DataEncoder class provides methods for encoding and decoding values:
class DataEncoder:
def __init__(self, Tmin=10.0, Tcod=100.0):
...
def encode_value(self, value: float) -> tuple[float, float]:
...
def decode_interval(self, spiking_interval: float) -> float:
...
Attributes:
| Attribute | Description |
|---|---|
Tmin | Minimum ISI (typically 10 ms) |
Tcod | Duration over which [0,1] is scaled (e.g., 100 ms) |
Tmax | Tmin + Tcod (maximum possible ISI) |
Integration
The DataEncoder is used during simulation and output processing:
from axon_sdk.simulator import Simulator
from axon_sdk.encoders import DataEncoder
encoder = DataEncoder(Tmin=10.0, Tcod=100.0)
spike_pair = encoder.encode_value(0.6) # returns (0.0, 70.0)
This spike pair can then be injected into the network, and the simulator will handle the timing based on the encoded intervals.
sim.apply_input_value(value=0.6, neuron=input_neuron)
Output Decoding
interval = spike2_time - spike1_time
decoded_value = encoder.decode_interval(interval)
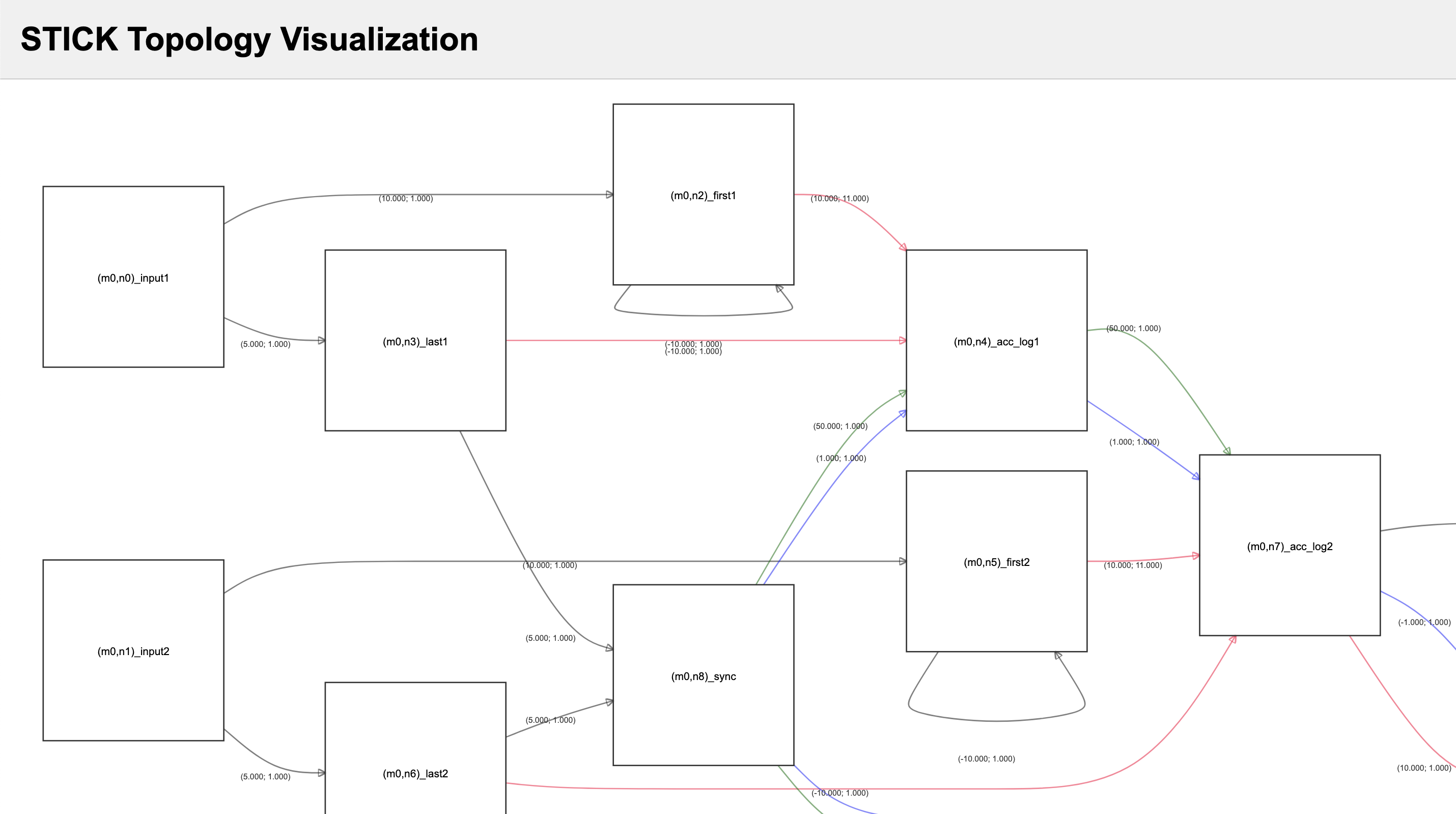
Visualization Tools in Axon SDK
Axon SDK provides two key visualization tools to understand spiking behavior and network topology:
- Chronogram Plotting — for spike timing and voltage trace analysis
- Interactive Topology Viewer — for structural exploration of STICK modules
These tools help debug and inspect both timing dynamics and network architecture.
1. Chronogram Plot (chronogram.py)
This tool visualizes the membrane voltage evolution and spike times across all neurons over time.
Key Functions
plot_chronogram(timesteps, voltage_log, spike_log)
- Draws voltage traces for each neuron
- Displays spike events as scatter points
- Labels neurons with their
uid(and optional metadata)
Each subplot shows:
V(t)trace of a neuron- Red dots for emitted spikes
- Gray gridlines and minimal axis clutter
An example plot might look like this:
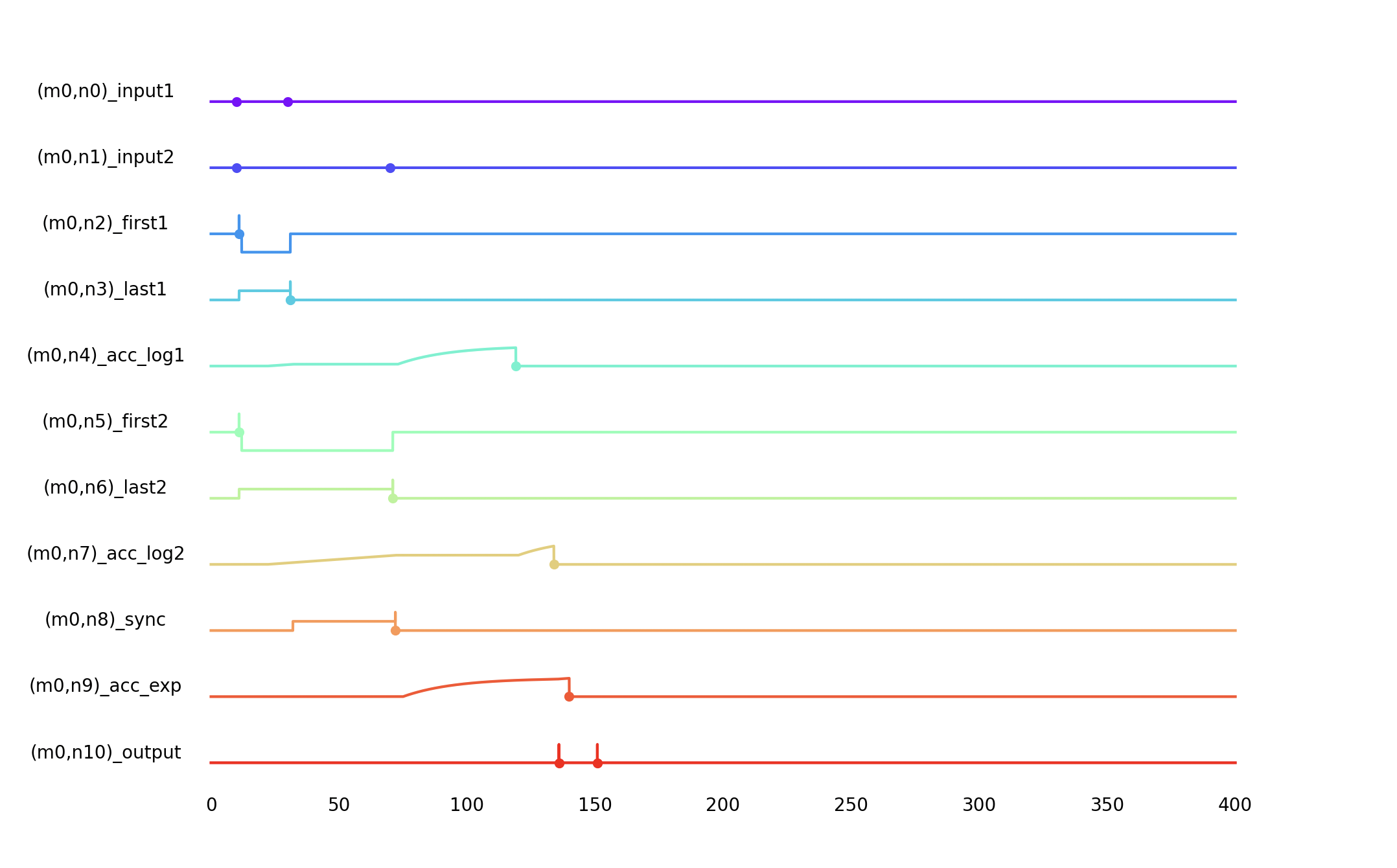
build_array(length, entry_points, fill_method='ffill')
Used to convert sparse voltage logs into dense time-series arrays using forward-fill or zero-fill.
Example Use
sim.plot_chronogram()
Here is the resulting chronogram plot:
Example Workflow
from axon_sdk.visualization import vis_topology, plot_chronogram
# Visualize network architecture
vis_topology(my_stick_network)
# After simulating
sim.plot_chronogram()
Compilation (compilation/compiler.py)
The compiler.py module is responsible for transforming a high-level symbolic computation expressed as a graph of Scalar operations into an executable STICK network composed of spiking neurons and synaptic connections. The resulting structure can be simulated, visualized, or deployed on neuromorphic hardware such as Ada.
The compiler performs the following steps:
- Flatten a scalar expression into nodes and connections
- Map each operation (
Add,Mul,Neg,Load) to a pre-built STICK subnetwork - Wire these modules together via excitatory synapses
- Generate input triggers and output readers
- Return an
ExecutionPlanfor simulation or deployment
Compilation Pipeline
The compilation process consists of several key stages:
Scalar Expression ↓ trace() + flatten() ↓ OpModuleScaffold list + Connection list ↓ spawn_stick_module() for each op ↓ fill_op_scafold() binds plugs to neurons ↓ instantiate_stick_modules() adds subnetworks ↓ wire_modules() connects neuron headers ↓ get_input_triggers() + get_output_reader() ↓ ExecutionPlan
Core Components
OpModuleScaffold
Represents one computation node (e.g. add, mul, load). Stores:
- Operation type (
OpType) - Input/output plugs
- Pointer to associated STICK module
Plug
A named handle to a specific scalar value or intermediate result. Later linked to neuron headers.
InputTrigger
Encodes a scalar input value (normalized to [0, 1]) and identifies the plus or minus neuron to inject.
OutputReader
Defines how to decode spike intervals from output neuron headers into scalar values.
ExecutionPlan
Holds the final network and all I/O mappings:
ExecutionPlan(
net=SpikingNetworkModule,
triggers=[InputTrigger, ...],
reader=OutputReader
)
Major Functions
-
flatten(root: Scalar)Flattens the computation graph and wraps nodes as OpModuleScaffold. Tracks dependencies as Connections. -
spawn_stick_module(op, norm)Creates a STICK subnetwork corresponding to the operation:
Add → AdderNetwork
Mul → SignedMultiplierNormNetwork
Load → InjectorNetwork
Neg → SignFlipperNetwork
Returns module + input/output neuron headers.
fill_op_scafold(op)Populates the scaffold:
Assigns STICK module to op.module
Binds input/output Plugs to NeuronHeaders
-
instantiate_stick_modules(ops, net, norm)Instantiates and attaches all submodules to the main SpikingNetworkModule. -
wire_modules(conns, net)Adds V-synapse connections between output and input neurons across modules. -
get_input_triggers(ops)Extracts Load operations and creates corresponding InputTriggers. -
get_output_reader(plug)Identifies the neuron header from the final output and wraps it into an OutputReader
Final Step: compile_computation(root: Scalar, max_range: float)
This function drives the full compilation process:
-
Flattens the symbolic expression
-
Builds and wires STICK modules
-
Extracts inputs and outputs
-
Returns an ExecutionPlan
plan = compile_computation(root=my_expr, max_range=50.0)
Example
from axon_sdk.primitives import DataEncoder
from axon_sdk.simulator import Simulator
from axon_sdk.compilation import Scalar, compile_computation
if __name__ == "__main__":
# 1. Computation
x = Scalar(2.0)
y = Scalar(3.0)
z = Scalar(4.0)
out = (x + y) * z
out.draw_comp_graph(outfile='basic_computation_graph')
# 2. Compile
norm = 100
execPlan = compile_computation(root=out, max_range=norm)
# 3. Simulate
enc = DataEncoder()
sim = Simulator.init_with_plan(execPlan, enc)
sim.simulate(simulation_time=600)
# 4. Readout
spikes_plus = sim.spike_log.get(execPlan.output_reader.read_neuron_plus.uid, [])
spikes_minus = sim.spike_log.get(execPlan.output_reader.read_neuron_minus.uid, [])
if len(spikes_plus) == 2:
decoded_val = enc.decode_interval(spikes_plus[1] - spikes_plus[0])
re_norm_value = decoded_val * 100
print("Received plus output")
print(f"{re_norm_value}")
if len(spikes_minus) == 2:
decoded_val = enc.decode_interval(spikes_minus[1] - spikes_minus[0])
re_norm_value = -1 * decoded_val * 100
print("Received minus output")
print(f"{re_norm_value}")
<title>Axon SDK API Reference — Axon SDK 0.1.0 documentation</title>
<link rel="stylesheet" type="text/css" href="_static/pygments.css?v=5ecbeea2" />
<link rel="stylesheet" type="text/css" href="_static/basic.css?v=b08954a9" />
<link rel="stylesheet" type="text/css" href="_static/alabaster.css?v=27fed22d" />
<script src="_static/documentation_options.js?v=01f34227"></script>
<script src="_static/doctools.js?v=9bcbadda"></script>
<script src="_static/sphinx_highlight.js?v=dc90522c"></script>
<link rel="index" title="Index" href="genindex.html" />
<link rel="search" title="Search" href="search.html" />
<link rel="next" title="axon_sdk package" href="axon_sdk.html" />
<div class="document">
<div class="documentwrapper">
<div class="bodywrapper">
<div class="body" role="main">
Axon SDK API Reference¶
Welcome to the API reference for the Axon SDK — a simulation framework for spike-timing-based neural computation using the STICK model.
This documentation includes modules for neuron models, synaptic primitives, network architecture, simulation, visualization, and compilation utilities.
</div>
</div>
</div>
<div class="sphinxsidebar" role="navigation" aria-label="Main">
<div class="sphinxsidebarwrapper">
Axon SDK
Navigation
Modules
- axon_sdk package
- axon_sdk.primitives package
- axon_sdk.networks package
- axon_sdk.compilation package
- axon_sdk.visualization package
</div>
</div>
<div class="clearer"></div>
</div>
<div class="footer">
©2025, Neucom ApS.
|
Powered by <a href="https://www.sphinx-doc.org/">Sphinx 8.2.3</a>
& <a href="https://alabaster.readthedocs.io">Alabaster 1.0.0</a>
|
<a href="_sources/index.rst.txt"
rel="nofollow">Page source</a>
</div>