Neuron Model in Axon
This document details the spiking neuron model used in Axon, which implements the STICK (Spike Time Interval Computational Kernel) computational paradigm. It emphasizes temporal coding, precise spike timing, and synaptic diversity for symbolic computation.
1. Overview
Axon simulates event-driven, integrate-and-fire neurons with:
- Millisecond-precision spike timing
- Multiple synapse types with distinct temporal effects
- Explicit gating to modulate temporal dynamics
The base classes are:
AbstractNeuron: defines core membrane equationsExplicitNeuron: tracks spike times and enables connectivitySynapse: defines delayed, typed connections between neurons
2. Neuron Dynamics
Each neuron maintains four internal state variables:
| Variable | Description |
|---|---|
V | Membrane potential (mV) |
ge | Persistent excitatory input (constant) |
gf | Fast exponential input (gated) |
gate | Binary gate controlling gf integration |
The membrane potential evolves according to:
\tau_m \frac{dV}{dt} = g_e + \text{gate} \cdot g_f
where:
τmis the membrane time constantg_eis the persistent excitatory inputg_fis the fast decaying input, gated bygateThe neuron spikes whenVexceeds a thresholdVt, at which point it emits a spike and resets its state. After a spike, the neuron resets:
V → Vreset ge → 0 gf → 0 gate → 0
This reset guarantees clean integration for subsequent intervals.
4. Synapse Types
Axon supports four biologically inspired synapse types:
| Type | Effect |
|---|---|
V | Immediate change in membrane: V += w |
ge | Adds persistent drive: ge += w |
gf | Adds fast decaying drive: gf += w |
gate | Toggles gate flag (w = ±1) to activate gf |
Each synapse also includes a configurable delay, enabling precise temporal computation.
5. Implementation Summary
Class: AbstractNeuron
- Implements update logic for
ge,gf, andgate - Defines
update_and_spike(dt)for simulation cycles - Supports
receive_synaptic_event(type, weight)
Class: ExplicitNeuron
- Inherits from
AbstractNeuron - Tracks:
spike_times[]out_synapses[]
- Implements
reset()after spike emission
Class: Synapse
- Defines:
pre_neuron,post_neuronweight,delay,type
- Used to construct event-driven spike queues with delay accuracy
6. Temporal Coding & Integration
This neuron model is designed for interval-coded values. Time intervals between spikes directly encode numeric values.
Integration periods in neurons align with computation windows:
ge: accumulates static value during inter-spike intervalgf+gate: used for exponential/logarithmic timingV: compares integrated potential to threshold for spike emission
These dynamics enable symbolic operations such as memory, arithmetic, and differential equation solving.
7. Numerical Parameters
Typical parameter values used in Axon:
| Parameter | Value | Meaning |
|---|---|---|
Vt | 10.0 mV | Spiking threshold |
Vreset | 0.0 mV | Voltage after reset |
τm | 100.0 ms | Membrane integration constant |
τf | 20.0 ms | Fast synaptic decay constant |
Units are in milliseconds or millivolts, matching real-time symbolic processing and neuromorphic feasibility.
8. Benefits of This Model
- Compact: Minimal neurons required for functional blocks
- Precise: Accurate sub-millisecond spike-based encoding
- Composable: Modular design supports hierarchical circuits
- Hardware-Compatible: Ported to digital integrate-and-fire cores like ADA
Neuron Model Animation
 This animation demonstrates how a single STICK neuron responds over time to different synaptic inputs. Each input type (
This animation demonstrates how a single STICK neuron responds over time to different synaptic inputs. Each input type (V, ge, gf, gate) produces distinct changes in membrane dynamics. The neuron emits a spike when its membrane potential V(t) reaches the threshold Vt = 10.0 mV, after which it resets.
Synapse Events Timeline
| Time (ms) | Type | Value | Description |
|---|---|---|---|
t = 20 | V | 10.0 | Instantaneously pushes V to threshold: triggers immediate spike |
t = 60 | ge | 2.0 | Applies constant integration current: slow, linear voltage increase |
t = 100 | gf | 2.5 | Adds fast-decaying input, gated via gate = 1 at same time |
t = 160 | V | 2.0 | Small, instant boost to V |
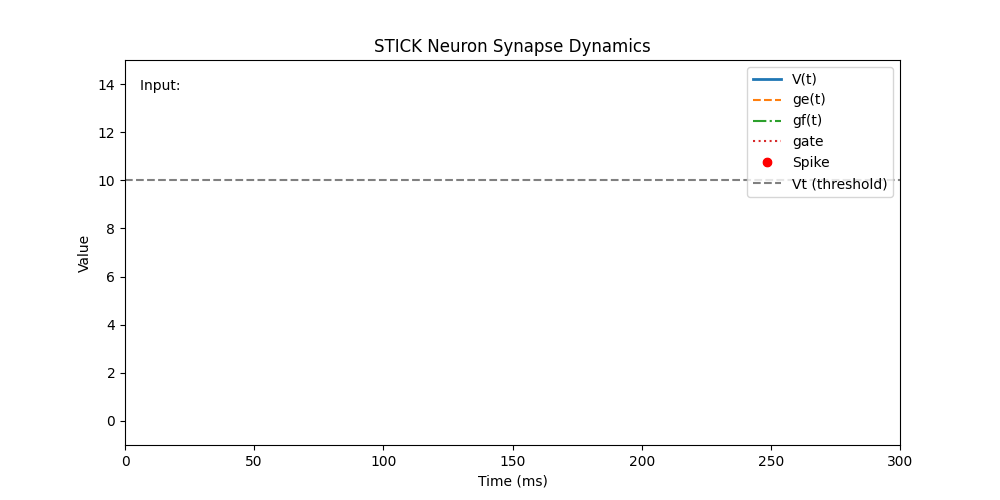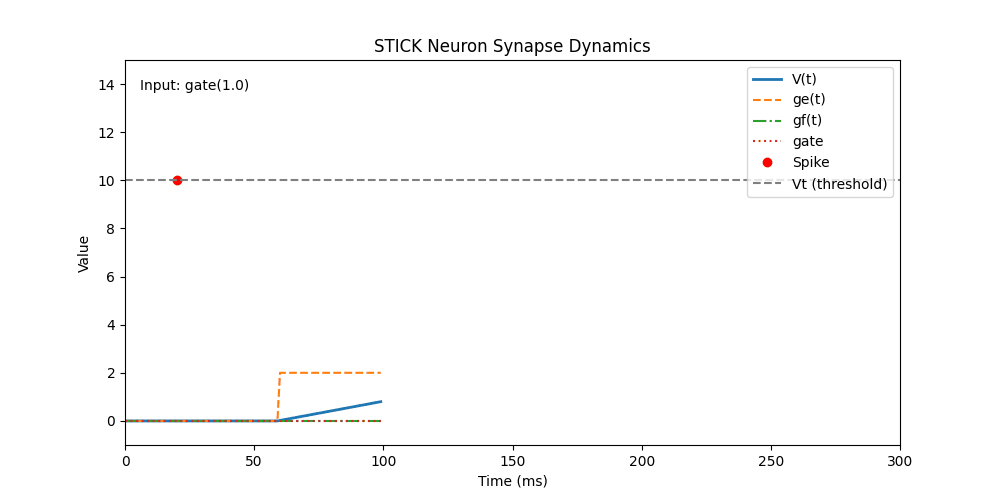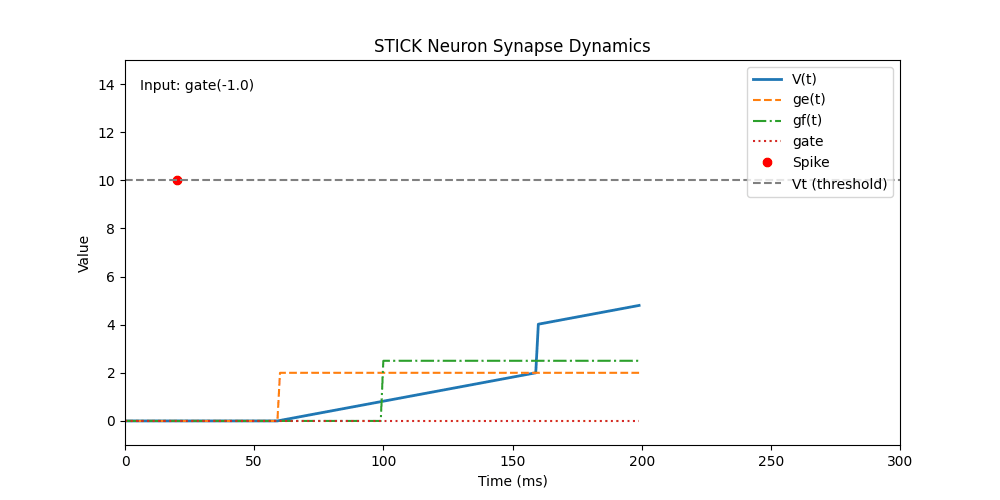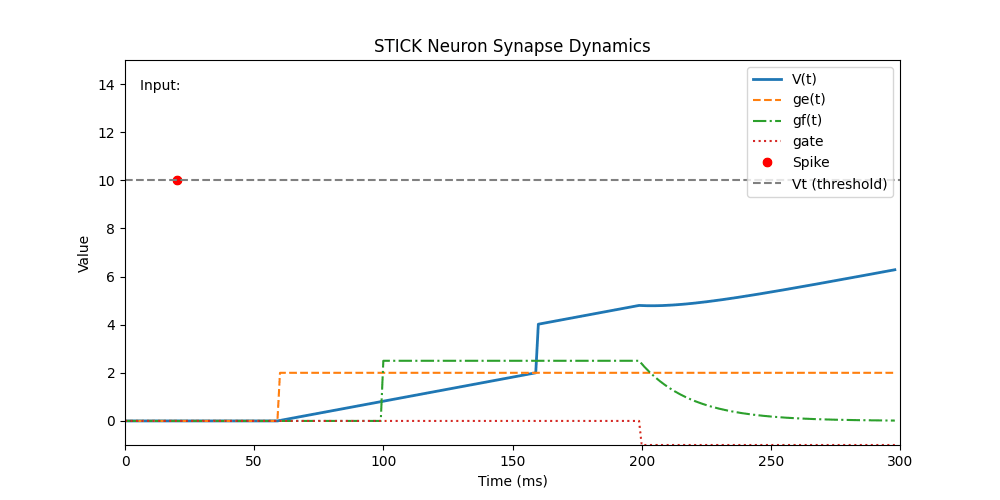
t = 200 | gate | -1.0 | Disables exponential decay pathway by zeroing the gate signal |
Event-by-Event Explanation
t = 20 ms — V(10.0)
- A V-synapse adds +10.0 mV to
Vinstantly. - Since
Vt = 10.0, this causes immediate spike. - The neuron resets:
V → 0,ge, gf, gate → 0.
Effect: Demonstrates a direct spike trigger via instantaneous voltage jump.
t = 60 ms — ge(2.0)
- A ge-synapse applies constant input current.
- Voltage rises linearly over time.
- Alone, this isn’t sufficient to reach
Vt, so no spike occurs yet.
Effect: Shows the smooth effect of continuous integration from ge-type input.
t = 100 ms — gf(2.5) and gate(1.0)
- A gf-synapse delivers fast-decaying input current.
- A gate-synapse opens the gate (
gate = 1), activatinggfdynamics. - Voltage rises nonlinearly as
gfinitially dominates, then decays. - Combined effect from earlier
geandgfcauses a spike shortly after.
Effect: Demonstrates exponential integration (gf) gated for a temporary burst.
t = 160 ms — V(2.0)
- A small V-synapse bump of +2.0 mV occurs.
- This is not enough to cause a spike, but it shifts
Vupward instantly.
Effect: Shows subthreshold perturbation from a V-type synapse.
t = 200 ms — gate(-1.0)
- The gate is closed (
gate = 0), disablinggfdecay term. - Any remaining
gfis no longer integrated intoV.
Effect: Demonstrates control logic: gf is disabled, computation halts.
Summary of Synapse Effects
| Synapse Type | Behavior |
|---|---|
V | Instantaneous jump in membrane potential V |
ge | Slow, steady increase in V over time |
gf + gate | Fast, nonlinear voltage rise due to exponential dynamics |
gate | Controls whether gf affects the neuron at all |
Spike Dynamics
When V ≥ Vt, the neuron:
- Spikes
- Logs spike time
- Resets all internal state to baseline
You can see these spikes as red dots at the threshold line in the animation.
References
- Lagorce & Benosman (2015): Spike Time Interval Computational Kernel
- Axon SDK Source:
- Neuron model:
axon/elements.py - Event logic:
axon/events.py - Simulator integration:
axon/simulator.py
- Neuron model: