Axon SDK Documentation

Functional Networks in Axon SDK

The axon_sdk.networks.functional module implements symbolic arithmetic and nonlinear operations using biologically inspired spiking neuron circuits. These circuits follow the STICK (Spike Time Interval Computational Kernel) framework, encoding and transforming values as spike intervals.

Included Functional Modules

Each of these networks is implemented as a subclass of SpikingNetworkModule.

Case Study: Exponential Function (exponential.py)

Purpose

implements the exponential function ( e^x ) using a spiking network.

Where x ∈[0,1] is encoded as a spike interval, and the network emits an output spike interval corresponding to e^x also encoded as an interspike time.

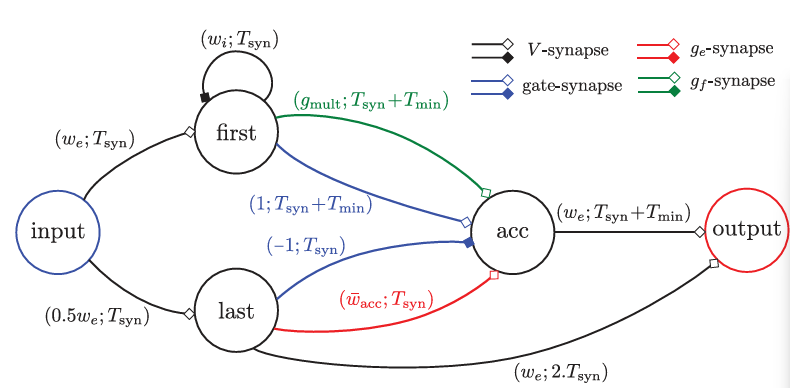
Construction

Principle

As described in the STICK paper (Lagorce et al. 2015) exponential encoding uses gated exponential decay to map input to output time:

tf * d/dt(gf) = -gf

The accumulated voltage V(t) rises under:

tm * dV/dt = gate * gf

• first activates gf on acc with delay Tmin, setting exponential decay in motion.
• gate=1 is enabled at the same time to allow gf to contribute to V(t).
• last disables gate (gate=-1) and adds a fixed ge to push acc towards the threshold and spiking.
• acc->output: Once V(t) exceeds threshold, output emits a spike with interval equal to the accumulated voltage.

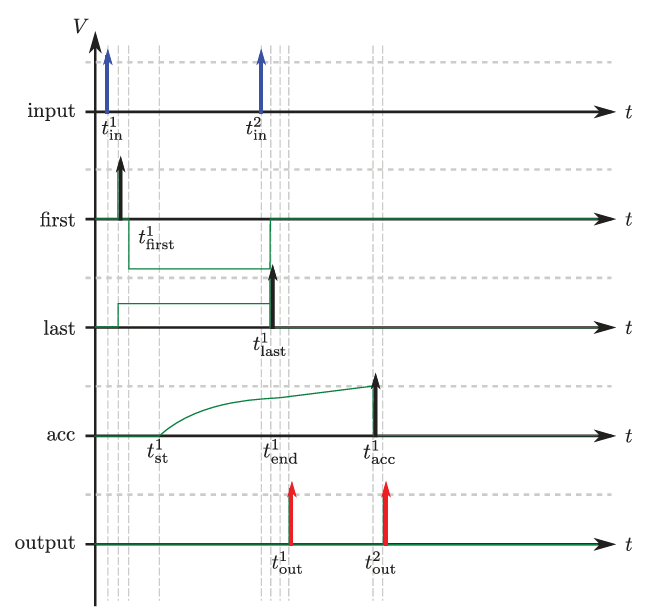
self.connect_neurons(self.first, self.acc, "gf", gmult, Tsyn + Tmin)
self.connect_neurons(self.first, self.acc, "gate", 1, Tsyn + Tmin)
self.connect_neurons(self.last, self.acc, "gate", -1.0, Tsyn)
self.connect_neurons(self.last, self.acc, "ge", wacc_bar, Tsyn)

The delay of the output spike is computed as:

$$ T_{\text{out}} = T_{\text{min}} + T_{\text{cod}} \cdot e^{-x \cdot T_{\text{cod}} / \tau_f} $$

This ensures that the spike interval output represents:

$$ y = e^x $$

encoded again via interspike time.

Simulation Result Example

Input value: 0.5
Expected exp value: 1.6487
Decoded exp value: 1.6332
Expected exp delay: 49.3 ms
Measured exp delay: 49.7 ms

Flow for Implementing New Stick Networks

1. Subclass SpikingNetworkModule

class MyNetwork(SpikingNetworkModule):
    def __init__(self, encoder, module_name=None):
        super().__init__(module_name)
        ...

2. Define neurons:

self.inp = self.add_neuron(Vt, tm, tf, neuron_name="inp")

3. Connect neurons with appropriate synapses:

• V: Jump voltage
• ge: Constant integration
• gf: Exponential
• gate: control input

self.connect_neurons(src, tgt, "ge", weight, delay)

Full Exponential Network Example

from axon_sdk.primitives import (
    SpikingNetworkModule,
    DataEncoder,
)
import math

from typing import Optional


class ExponentialNetwork(SpikingNetworkModule):
    def __init__(self, encoder: DataEncoder, module_name: Optional[str] = None) -> None:
        super().__init__(module_name)
        self.encoder = encoder

        # Parameters
        Vt = 10.0
        tm = 100.0
        self.tf = 20.0
        Tsyn = 1.0
        Tmin = encoder.Tmin

        we = Vt
        wi = -Vt
        gmult = (Vt * tm) / self.tf
        wacc_bar = Vt * tm / encoder.Tcod  # To ensure V = Vt at Tcod

        # Neurons
        self.input = self.add_neuron(Vt, tm, self.tf, neuron_name="input")
        self.first = self.add_neuron(Vt, tm, self.tf, neuron_name="first")
        self.last = self.add_neuron(Vt, tm, self.tf, neuron_name="last")
        self.acc = self.add_neuron(Vt, tm, self.tf, neuron_name="acc")
        self.output = self.add_neuron(Vt, tm, self.tf, neuron_name="output")

        # Connections from input neuron
        self.connect_neurons(self.input, self.first, "V", we, Tsyn)
        self.connect_neurons(self.input, self.last, "V", 0.5 * we, Tsyn)

        # Inhibit first after spike
        self.connect_neurons(self.first, self.first, "V", wi, Tsyn)

        # Exponential computation:
        # 1. First spike → apply gf with delay = Tsyn + Tmin
        self.connect_neurons(self.first, self.acc, "gf", gmult, Tsyn + Tmin)
        self.connect_neurons(self.first, self.acc, "gate", 1, Tsyn + Tmin)
        # 2. Last spike → open gate
        self.connect_neurons(self.last, self.acc, "gate", -1.0, Tsyn)

        # 3. Last spike → add ge to trigger spike after ts
        self.connect_neurons(self.last, self.acc, "ge", wacc_bar, Tsyn)

        # Readout to output
        self.connect_neurons(self.acc, self.output, "V", we, Tsyn + Tmin)
        self.connect_neurons(self.last, self.output, "V", we, 2 * Tsyn)


def expected_exp_output_delay(x, encoder: DataEncoder, tf):
    try:
        delay = encoder.Tcod * math.exp(-x * encoder.Tcod / tf)
        Tout = encoder.Tmin + delay
        return Tout
    except:
        return float("nan")


def decode_exponential(output_interval, encoder: DataEncoder, tf):
    return ((output_interval - encoder.Tmin) / encoder.Tcod) ** (-tf / encoder.Tcod)


if __name__ == "__main__":
    from axon_sdk import Simulator

    encoder = DataEncoder(Tmin=10.0, Tcod=100.0)
    net = ExponentialNetwork(encoder)
    sim = Simulator(net, encoder, dt=0.01)

    value = 0.5
    sim.apply_input_value(value, neuron=net.input, t0=10)
    sim.simulate(150)

    output_spikes = sim.spike_log.get(net.output.uid, [])
    if len(output_spikes) == 2:
        out_interval = output_spikes[1] - output_spikes[0]
        print(f"Input value: {value}")
        print(
            f"Expected exp value: {math.exp(value)}, decoded exp value {decode_exponential(out_interval, encoder, net.tf)}, "
        )
        print(
            f"Expected exp delay: {expected_exp_output_delay(value, encoder, net.tf):.3f} ms"
        )
        print(f"Measured exp delay: {out_interval:.3f} ms")
    else:
        print(f"Expected 2 output spikes, got {len(output_spikes)}")